Employer wage-setting, or monopsony, power has received renewed attention in recent years among researchers and policymakers. This literature review summarizes relevant parameters and techniques for measuring the extent of labor market monopsony and discusses estimates of the earnings effects of monopsony, with particular attention paid to employer concentration (or consolidation) and health care labor markets. While I have done my best to include all of the most relevant recent studies related to employer market power and concentration, the rapid growth of this literature likely means that some papers have been inadvertently omitted.
The key parameter for measuring the degree of monopsony power available to employers is the elasticity of labor supply to the firm. I briefly discuss the underlying theory behind this elasticity in Section 2 and show why it represents what Bronfenbrenner (1956) called “potential monopsony power.” Intuitively, this parameter measures how sensitive employment at a given employer is to changes in the wage that it pays. If the employer reduced wages by a small amount and all of its workers left to work elsewhere, then the elasticity of labor supply to the firm is infinite and the employer operates in a perfectly competitive labor market. If, on the other hand, at least some of the workers stayed then this elasticity is finite, and the employer is said to have some degree of wage-setting or market power.
Measuring this elasticity using the most robust methodology requires linked employer-employee data which is typically not publicly available. As a result, renewed interest in antitrust policy as a means to increase competition in the labor market, together with barriers to directly measuring employer power, has led researchers in recent years to (re)turn to labor market concentration as a way to characterize potential wage-setting power. I discuss how labor market concentration is related to monopsony power in Section 3. Concentration is a potential source of monopsony power, but it does not itself measure the extent to which employers are able to pay workers below their marginal value to the firm (or marginal revenue product of labor). Because concentration does not arise exogenously and is the result of market forces, it is also the case that an increase in concentration does not automatically imply that wages will decrease. Researchers should therefore be careful to note that the relationship between wages and concentration is not causal, even when it is estimated using instrumental variables. It is also important to provide the appropriate institutional context and a theory for how one expects concentration to affect labor market competition and be negatively correlated with wages in a given setting.
I next discuss recent estimates of the relationship between concentration and wages, as well as other labor market outcomes, in Section 4. This literature consistently finds that concentration is negatively correlated with posted wages, earnings, compensation, and hiring. However, some papers also demonstrate that concentration has little correlation with direct measures of employer power in some contexts. These results again point to the fact that the correlation between concentration and wages does not reflect a causal relationship. This section also describes both the variety of local labor market definitions and instruments for local concentration used in these studies.
Section 5 then turns to the health care industry and discusses estimates of monopsony and the effects of labor market concentration in this sector. The health care labor market, especially for hospital personnel such as nurses, is likely to be monopsonistic because hospitals often operate in sparse markets and industry-specific training can limit the outside options of many workers. Indeed, existing estimates of the elasticity of labor supply to the firm within the health care industry reveal substantial amounts of employer market power. In addition, I discuss some of the most compelling evidence for how consolidation impacts employer market power and wages for hospital workers (Prager and Schmitt, 2021). Finally, Section 6 discusses the lessons for researchers interested in using concentration to study labor market monopsony.
Monopsonistic labor markets, unlike those operating under perfect competition, are characterized by a labor supply curve to an individual firm that is not infinitely elastic. As a result, the “most direct” way to measure the extent of monopsony is to estimate the elasticity of the labor supply curve to individual firms (Manning, 2021). In the simple, static model of monopsony, employers face a revenue function F(N) and a labor supply curve N(w) . Then the first-order condition that governs the profit-maximizing wage can be written as:

Here, MRP is the marginal revenue product of labor, w is the wage, and ƐNw is the elasticity of labor supply to the firm.1 This elasticity indicates how responsive are the workers at a specific firm to changes in the wage that the firm pays, and it is equal to the percent change in the number of workers at the firm divided by the percent change in the wage paid by the firm. In a perfectly competitive labor market, workers are easily able to move between jobs and therefore are highly sensitive to changes in the wage paid by their employer. In that case, the elasticity of labor supply to the firm is infinite: ƐNw = ∞. An infinite elasticity means that, if their employer cuts the wage by even one penny, all of the workers would leave that firm and work elsewhere. On the other hand, in an imperfectly competitive (or monopsonistic) labor market, the elasticity of labor supply to the firm is less than infinity, or finite. A finite elasticity means that some but not all workers will leave the firm if it cuts its wage. Therefore, smaller values of the elasticity of labor supply to the firm indicate that the labor market is less competitive and more monopsonistic.
Sokolova and Sorensen (2021) show that (1) can also be re-written as:

Under perfect competition (ƐNw = ∞), the last worker hired will be paid exactly their marginal product. Suppose instead that ƐNw = 9. Then the wage will be equal to 90% of the marginal product, a 10% markdown from what the wage would be under perfect competition. It therefore seems appealing to directly estimate ƐNw. One way that researchers have approached this is with regressions of the form:
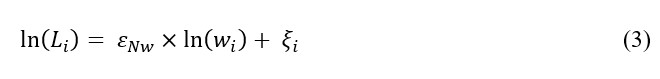
Here, Li is the number of workers employed by the firm and wi is the wage. But as noted by Manning (2011, 2021), it can be difficult to find credibly exogenous variation in wages at a single firm that does not affect the labor market as a whole. For example, Staiger et al. (2010) and Falch (2010) study plausibly exogenous changes in public sector wages in hospitals and schools, respectively, to estimate labor supply elasticities for individual employers and find very small elasticities: ƐNw < 2 in both cases, implying a wage markdown of at least one-third.
These estimated elasticities are so small that Manning (2011) suggests that they suffer from biases related to their short time horizon, expectations of whether the wage changes are temporary or permanent, and most importantly, not allowing for employers to respond using non-wage channels (such as devoting more resources to hiring additional workers). This third critique, that firms can respond to mandated wage changes using other channels and still be monopsonistic, is outlined further in Manning (2006). It also means that quasi-experimental estimates of ƐNw from policy changes are potentially unable to identify the true underlying parameter, the elasticity of labor supply to the firm, that these studies attempt to measure.
Instead, Manning (2003) suggests estimating the elasticity of labor supply to the firm based on the rates of recruitment to and separation from the firm. The intuition behind this type of model is that frictions, in the form of search costs for employers and imperfect mobility between jobs for workers, cause labor markets to depart from the competitive benchmark. Manning (2003) describes a simple dynamic search model based on Burdett and Mortensen (1998) where workers leave the firm at rate s and recruits arrive at the firm at rate R. The separation rate is negatively correlated with the wage and the recruitment rate is positively correlated with the wage. Suppose the firm employed Nt-1 workers last period and pays a wage wt this period. Then its current supply of labor, Nt, is:
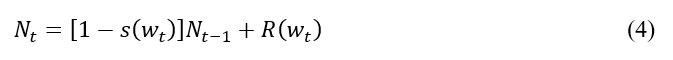
where s(wt) is the separation rate and R(wt) is the recruitment rate. In steady state, where the employment level at the firm is constant, the total number of separations (given by s(w) x N(w)) must equal the total number of recruits (R(w)). This steady state relationship gives us an expression for the long-run positive relationship between employment and wages:

This relationship allows us to write the elasticity of labor supply to the firm as:

where ƐRw is the elasticity of recruits with respect to the wage and Ɛsw is the elasticity of separations with respect to the wage.2
The expression in (6) shows that researchers can recover the elasticity of labor supply to the firm in a way that avoids the pitfalls associated with studies of mandated wage changes described above. Unfortunately, data on both recruitment intensity and separations is difficult to obtain. As a result, Manning (2003) suggests using the fact that, in steady state, the separation elasticity should be equal to the opposite of the recruitment elasticity: Ɛsw = -ƐRw. Then the elasticity of labor supply to the firm can be estimated as:

which can be readily estimated with appropriate data.
Sokolova and Sorensen (2021) conducted a meta-analysis of more than 1,000 estimates of the elasticity of the labor supply to the firm. Their sample includes estimates using both the static model implied by (1) and (3) as well as the separations-based approach given by (7). The authors find substantial evidence of imperfect competition in the labor market. The estimates they identify as following best practices range from 6.4 to 9.9 based on the elasticity of separations and at least 20 based on the static model. Assuming that firms were able to fully markdown wages according to these elasticity estimates, then the range of estimates from Sokolova and Sorensen (2021) imply that workers are paid between 9% and 13% less than their value to their employers (based on the separations elasticity). The authors note that the relatively large difference in elasticities produced by the two methods likely results from unobserved supply shocks creating upward bias in estimates from the static model, as discussed in Manning (2003).
The majority of these estimates studied by Sokolova and Sorensen (2021), including those with the best identification strategies, are based on the separations elasticity. Indeed, Manning (2003) provides straightforward instructions for estimating the necessary parameters and avoiding common pitfalls, provided one has the necessary data. The data, however, are where much of the difficulty of producing estimates of the elasticity of labor supply to the firm lies. The approach outlined by Manning (2003) requires linked employer-employee data, which in almost all cases is not publicly available. In addition, analyses of the elasticity of labor supply to the firm are not always readily linked to policy remedies. Researchers in recent years, therefore, have returned to an older method of characterizing potential market power, labor market concentration, which has a more direct connection to antitrust policy but is also not without its own drawbacks.3
Labor market concentration is a potential source of employer wage-setting power (see, e.g., Boal and Ransom, 1997; Azar et al., 2019b). The theoretical underpinning of this relationship relies on so-called Cournot models of competition. In these models, a single market wage increases with the level of employment in the market. Each Firm chooses how many workers to employ in order to maximize its profits while taking as given the employment levels of all other firms in the same labor market and therefore anticipating that higher levels of employment lead to a higher wage being paid by all employers in the labor market, including itself.
As discussed in Boal and Ransom (1997) and Azar et al. (2019b), firms maximize their profits by choosing the number of workers to employ (Li) in order to satisfy the following equality between the additional revenue generated by the last worker hired and the cost of employing them:

Here, MRPi is the marginal revenue product of labor for firm i, w is the single market wage, (Li/L) is firm i‘s market share of total employment (L), and is the market-level elasticity of labor supply.4 The left-hand side of equation (8) is the proportional gap between the marginal revenue product and the wage. This term is sometimes referred to as the firm-specific rate of exploitation, Ei. Importantly, the firm-specific rate of exploitation can also be shown to equal the inverse of the elasticity of labor supply to the firm (Manning, 2003). As discussed in Section 2, larger values of the elasticity of labor supply to the firm (or alternatively, smaller values of its inverse) correspond to increasing amounts of competition in the labor market, with an infinite elasticity indicating perfect competition.
In equation (8), therefore, we have a term that is proportional to a direct measure of monopsony power equal to a term that contains a firm’s market share and the market elasticity of labor. To move from a single firm’s market share to a measure of concentration in the labor market as a whole, we can take an employment-weighted average of Ei:
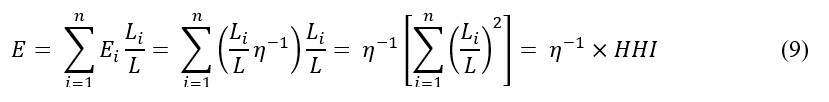
Now the term in brackets is the sum of squared market shares, which is the Herfindahl-Hirschman Index (HHI) for employment. The HHI is a commonly used measure of market concentration, including by the Department of Justice and the Federal Trade Commission in antitrust enforcement (U.S. Department of Justice, 2018). The index ranges from 0 to 1 with smaller values indicating a large number of firms of relatively equal size and larger values indicating fewer firms controlling more of the market.5 The HHI will increase if both the number of firms in the market decreases and the difference in the sizes of the remaining firms increases (i.e., becomes more asymmetric). Federal agencies consider markets with an HHI between 0.15 and 0.25 to be moderately concentrated and markets with an HHI greater than 0.25 to be highly concentrated (U.S. Department of Justice, 2018).6
As discussed above, E is also equal to the market-share weighted average of the inverse of the elasticity of labor supply to the firm. Thus, the average firm-level elasticity of labor supply in a given labor market is negatively correlated with the concentration of employment, as measured by the HHI, in that market (Boal and Ransom, 1997; Azar et al., 2019b). This relationship implies that, for a given marginal revenue product of labor, wages will be lower either when concentration is higher or when the average inverse firm-level elasticity of labor supply is smaller (Azar et al., 2019b).
However, while we can derive this relationship between concentration and the average elasticity of labor supply to the firm in a static setting, concentration as a measure of monopsony is not without its flaws. One downside to concentration is that it is a market outcome itself and is therefore determined by the same market forces that also determine wages. This has long been noted in the industrial organization literature (e.g., Bresnahan, 1989). Miller et al. (2021) provide a simple numerical example to illustrate the problem. They point out that lower costs incurred by the most efficient firms and increases in costs incurred by the least efficient firms can both increase the HHI by making market shares less symmetric while having different effects on prices, holding other factors constant. The result is that the relationship between prices and the HHI is theoretically ambiguous and so regressions estimating this relationship are unable to give us the causal effect necessary for predicting how consolidation impacts competition. In addition, instrumental variables are also unable to circumvent fully the issue described above. Because the HHI and wages are both determined by supply and demand (and the various factors that influence them), it is not possible to fully isolate variation in one variable in order to determine how it causes changes in the other.
Another drawback to concentration is that it may not always be indicative of market power. As noted by Manning (2021), in the search model of Burdett and Mortensen (1998), which is commonly used in modern dynamic monopsony models, there is a positive correlation between competition in the labor market and concentration. In this model, competition is measured by the arrival rate of job offers, and increased competition allows workers to move more easily from low-wage firms to high-wage firms, which in turn increases the market share of the high-wage firms.7
While concentration is only a potential source of monopsony power and may not even consistently indicate a lack of competition, recent empirical findings indicate that increased consolidation in the labor market is associated with worse outcomes for workers. As discussed in more detail in Section 4, increases in concentration are associated with lower posted wages, lower earnings, lower total compensation, and fewer new hires, all of which is consistent with the theoretical predictions from increases in employer power.
In addition, Azar et al. (2019a) empirically test the hypothesis that monopsony, as proxied by concentration, can explain why the employment effect of increasing the minimum wage is frequently found to be very close to zero. Using data on online job vacancies in the low wage retail industry, they find that more concentrated labor markets experience more positive employment effects from the minimum wage. In fact, the employment elasticity is the most negative in markets with the least amount of concentration and is actually positive in highly concentrated markets. This pattern of findings aligns with the prediction that monopsony can explain null or positive employment effects in the minimum wage literature. In the specific context studied by Azar et al. (2019a), therefore, it appears that concentration at least partially contributes to employer power in the labor market.
In this section, I review the recent literature on labor market concentration and organize the discussion around the various types of data employed by the authors.
4.1 Online Job Boards
Data from online job boards allow researchers to construct concentration measures using the number of vacancies and relate them to posted wages. Azar et al. (2019b) and Azar et al. (2020b) were the first to use this type of data, drawing from CareerBuilder which is one of the largest online job boards in the US. They construct vacancy shares and HHIs for labor markets defined as the combination of occupations (6-digit SOC codes) and commuting zones. They find that the average labor market is highly concentrated with an HHI of 0.32, but that concentration varies across markets with more populous commuting zones being less concentrated. The authors also estimate a negative relationship between concentration and posted wages. They instrument for the vacancy HHI in a given market using the inverse number of employers that post vacancies for the same occupation in other commuting zones in the same quarter, which allows them to exploit national-level changes in occupation-specific hiring over time. Their preferred IV specification leads to an estimated elasticity of the posted wage with respect to the vacancy HHI of -0.13. Moreover, moving from the 25th percentile to the 75th percentile of the distribution of concentration is associated with 17% lower posted wages.
In a similar study, Azar et al. (2020a) use data from Burning Glass Technologies in 2016, which claims to represent a near-universe of US online job vacancies, to estimate vacancy HHIs and wage elasticities. Labor markets are once again defined using occupations (SOC-6) and commuting zones. With the caveat that the Burning Glass data is only from one year, they find a higher level of concentration (0.44) for the average market than with the data from CareerBuilder. The correlation between vacancy HHIs and posted salaries is -0.16 while controlling for market-level employment (using data from the Bureau of Labor Statistics Occupational Employment Statistics). The authors also estimate correlations using only variation across occupations while holding commuting zones fixed. This exercise removes any omitted variable bias stemming from differences in populations across labor markets. These estimates (-0.12) are quite similar to the cross-market estimates, which helps allay concerns about the estimates being primarily driven by more rural labor markets.
Schubert et al. (2021) also use vacancy data from Burning Glass to estimate the effect of concentration on wages, but they depart from Azar et al. (2020a) by defining local labor markets using observed occupation-to-occupation flows. More specifically, the authors supplement the occupation-by-geography labor market definition used elsewhere in the literature by constructing an index of wages in other occupations but within their own metropolitan areas. The wages in these other occupations are weighted by observed flows across occupations from actual résumés submitted to Burning Glass. The authors estimate that moving from the median to the 95th percentile of concentration is associated with a 3% reduction in wages and that there is substantial heterogeneity in the effect of concentration depending on the relative mobility of a worker’s occupation. The effect of concentration is around four times larger for workers in low outward mobility occupations compared to highly outward mobile occupations.
4.2 Census Data
While vacancies can represent the options available to employers at a given point in time, it is unclear how these vacancies translate into actual employment. As a result, a number of studies have constructed HHIs using employment data from the U.S. Census Bureau.8 Relying on Census data also means that the authors need to define local labor markets in a slightly different way, using industries in combination with geographies. Rinz (2020) uses data from the Longitudinal Business Database (LBD) to document trends in local labor market concentration going back to the 1970s. He defines labor markets as the combination of industries (4-digit NAICS codes) and commuting zones, and constructs employment-based HHIs for each market. In contrast to popular narratives, Rinz (2020) finds that while national concentration has risen over the last several decades, average local concentration has actually fallen over the same time: in 2015, average local concentration (approximately 0.15) was about 25% lower than in 1976 (approximately 0.20). In other words, while there are fewer companies operating in the average industry nationwide, they are more likely to be competing against each other in the average local labor market.
He also estimates descriptive regressions relating earnings and concentration, instrumenting for a given market’s HHI with the average HHI experienced by workers in the same industry but in other commuting zones. Over the period 1976 to 2015, the estimated earnings elasticity is a statistically significant -0.05, which corresponds to a 15% decrease in earnings when moving from the HHI experienced by the median worker to that experienced by a worker at the 75th percentile. However, as noted by Rinz (2020), the typical change in concentration within a market was much smaller than this and corresponds to a decrease in earnings of about 2%. Focusing in on more recent years (2005 to 2015), he estimates that the earnings elasticity is about -0.03 and corresponds to a decrease in earnings of about 1% for a typical within-market change in concentration over this period. The previous estimates are all weighted by total employment in the market. Without weights, the elasticity is much larger (-0.11) implying that concentration matters much more in smaller markets.
In a similar study, Benmelech et al. (2020) also use data from the LBD to estimate the effect of local concentration on wages in the manufacturing sector.9 They supplement their analysis with measures of establishment-level productivity from the Census of Manufacturers and the Annual Survey of Manufacturers in order to control for this aspect of wage determination. The authors also find a negative elasticity between concentration and wages of -0.01 from 1978 to 2016. They report that moving from one standard deviation below the average HHI to one standard deviation above it corresponds to a decrease in wages of about 3%. These results are robust to including a variety of fixed effects as well as the controls for plant-level productivity. They depart from other papers in the concentration literature by using merger activity to instrument for local concentration. Their estimates with the merger instrument are larger than those without it (the elasticity is between -0.03 and -0.06), with moves from a standard deviation below to a standard deviation above the average level of concentration corresponding to wage decreases of between 9% and 14%.
The authors also note that their estimated elasticity between concentration and wages becomes more negative over the course of their sample, consistent with declining bargaining power of manufacturing workers over this period. To empirically test whether this is the case, Benmelech et al. (2020) compare establishments that operate in industries with varying levels of unionization. They find that in industries with essentially zero unionization, the elasticity between concentration and wages is -0.02 whereas at average levels of unionization the elasticity is smaller by between 29% and 45%. This pattern also suggests that concentration and employer market power are positively related.
In contrast, Hershbein et al. (2020) estimate a plant-level measure of wage markdowns in the manufacturing sector and find only a small correlation between markdowns and concentration. This weak relationship suggests that local concentration is an imperfect proxy for labor market power. More specifically, the authors estimate the gap between the output elasticity of labor, or marginal revenue product of labor, and the revenue share of labor and use these wage markdowns as indicators of employer market power. They find substantial amounts of market power: a worker employed at the average plant earns about 65 cents for every dollar generated on the margin. Employer market share is also strongly associated with markdowns which lends support to size-based explanations for market power.
However, when looking at trends over time in aggregate markdowns and local concentration, the authors find that their aggregation of plant-level markdowns does not follow the same pattern as average local concentration. In particular, aggregate markdowns are falling since the 1970s and then sharply increase after the early 2000s. The trend in local concentration, on the other hand, does not follow this same path.10 Moreover, more concentrated markets do not exhibit higher markdowns, on average.11 The authors note that this apparent divergence between markdowns and concentration illustrates the challenges associated with aggregating micro-level estimates of market power into comprehensive market-level measures, such as HHIs, at least in the manufacturing industry.
Arnold (2021), meanwhile, takes a different approach than much of the concentration literature by looking directly at changes to concentration that arise from employer consolidation. He uses linked employer-employee data from the Census Bureau’s Longitudinal Employer-Households Dynamics (LEHD) program to study the direct effects of mergers and acquisitions (M&A) on workers in the parties to the merger as well as indirect effects on other workers in the same labor market. A key contribution of this paper relative to other studies in the concentration literature is the use of a concentration index which accounts for the substitutability of jobs across industries within commuting zones.12 Using a differences-in-differences design that matches workers in M&A firms with comparable workers that are not party to a merger, he finds that annual earnings fall by 2.1% relative to the control group after consolidations that led to large increases in local concentration. In contrast, mergers that had little impact on labor market concentration also had little impact on earnings, suggesting that the earnings decline is not entirely due to changes in productivity or product market concentration.
However, Arnold (2021) also notes that only 1.4% of the variation in concentration during his sample is due to changes in ownership with the rest attributable to expansions and contractions of existing firms. This pattern of results reinforces the need for care when describing the relationship between concentration and wages in cross-industry studies. Research that focuses on a single sector, such as the work on the health care industry described in Section 5, is able to make stronger claims about the relationship between concentration and imperfect competition in the labor market.
4.3 Other Data Sources
Qiu and Sojourner (2019) combine publicly available data from the Census Bureau with private data from Dun & Bradstreet (D&B) in order to assess the role of product market concentration in combination with labor market concentration on wages and compensation. The D&B data includes establishment-level location and employment as well as total firm sales. The authors then use the national occupation distribution for each industry and year (obtained from the Census Bureau) to map the D&B establishment-level employment into expected establishment-occupation employment shares. They conduct this exercise in order to create local labor markets defined as the combination of occupations and metropolitan areas. This methodology, which is necessary absent occupation-specific data, introduces measurement error into their employment HHIs.
The authors then relate their employment HHIs and product market HHIs (derived from firm-level sales shares in each metropolitan area) to worker-level characteristics from the American Community Survey (ACS). The ACS allows for controls related to workers’ human capital as well earnings and compensation. Instrumenting for local labor market concentration using the log of the inverse number of employing firms for the same occupation in other areas, they estimate that a one standard deviation increase in labor market concentration is associated with 14% lower wages (the elasticity is -0.14). They also find evidence that workers in more concentrated labor markets are less likely to be covered by health insurance, but this likely stems from substantial differences in insurance coverage across industries.
All of the studies discussed above use data from the US, but some research has also studied the effects of concentration in other countries as well.13 For example, Marinescu et al. (2021) study the effects of both labor and product market concentration in France. They define local labor markets using occupations and commuting zones and instrument for quarterly HHIs using the inverse number of employers in other commuting zones for the same occupation and quarter. The authors estimate that a 10% increase in concentration is associated with a 0.5% decrease in wages for new hires after including local labor market, worker, and firm fixed effects. Similar to Benmelech et al. (2020), the effects of concentration are somewhat mitigated in markets with relatively higher unionization.14 Marinescu et al. (2021) also find a negative relationship between labor market concentration and the number of new hires: a 10% increase in concentration is associated with 3.3% fewer new hires. These negative wage and hiring elasticities, which are robust to including controls for product market concentration, are consistent with predictions from oligopsony theory.
Another study in an international context is Jarosch et al. (2019), which uses data from Austria. The main contribution of this paper is the development of a search model of the labor market in which the average wage in a given market is a function of the employment concentration in the market as measured by an index that is very similar to the HHI.15 An important implication from their model is that average wages (at the market level) are decreasing and strictly concave in concentration. In other words, a given change in concentration will have different-sized effects on the wage depending on the baseline level of concentration with small changes having the largest negative effects in relatively more concentrated markets. Using labor markets defined based on observed flows of workers between firms using the techniques in Nimczik (2020), the authors estimate that employment (and productivity) concentration decrease the Austrian labor share by about 10%. Finally, Dodini et al. (2020) use data from Norway to estimate the effect of concentration as measured by the employment shares of relative skill groups within a market on wages. The authors use mass layoffs and plant closings as exogenous shocks to labor demand and find that workers in relatively more concentrated “skill clusters” have worse outcomes.
Economists have long looked to the health care industry as an example of where monopsonistic labor markets are likely to occur. As discussed in Matsudaira (2014b), this attention is due to the fact that many hospitals operate in areas with few competitors and the geographic and occupational mobility of some health care workers, in particular registered nurses, can be quite limited. Boal and Ransom (1997) and Manning (2003, 2011) review several of these studies on nursing labor markets. The earliest of these studies, going back to the 1970s, compare wages for nurses with hospital market concentration and find large, negative correlations. But these estimates suffer from poor research designs with insufficient controls to claim a causal relationship, and later studies show that they are not robust to controls for market size.
Despite the problems with older studies, there is still reason to believe that health care labor markets are likely characterized by substantial employer power. Manning (2003), for example, points to particular market phenomena that are suggestive of monopsony and which Matsudaira (2014b) notes are at least partially present in the market for nurses. These include persistent vacancies, employer provision of general (i.e., non-firm specific) training, and pay dispersion across firms for similar workers. In the remainder of this section, I discuss more recent studies that attempt to measure the actual extent of monopsony power in nursing and other health care labor markets.
Two studies have attempted to directly estimate the elasticity of labor supply to the firm using policy changes that affected the health care industry. Staiger et al. (2010) use a mandated increase in pay at Veteran Affairs (VA) hospitals to estimate firm-level elasticities for registered nurses. Their analysis is motivated by a model of competition in which hospitals only compete directly with other geographically proximate hospitals. This framework implies that non-VA hospitals will change their wages in response to the change at VA hospitals and that the size of this change will be largest for those closest to VA hospitals. Their empirical results confirm that there is considerable employer wage-setting power in the market for nurses. The authors estimate that a 10% increase in wages at the VA hospital causes wages at non-VA hospitals to increase by 2% at hospitals within 15 miles and 1% at hospitals within 15-30 miles of the focal VA hospital. They also estimate an average short-run (one year) elasticity of labor supply to a given hospital of 0.1, which indicates a substantial amount of monopsony power.
Matsudaira (2014a), meanwhile, uses an entirely different type of policy change to estimate the firm-level labor supply elasticity for low-wage nursing home aides. He uses a California law that changed minimum staffing requirements at nursing homes to study how wages change after employers are forced to hire more workers. He finds that nursing homes which were out of compliance with the new law did not have to increase their wage offers relative to those that were not bound by the policy change, which, in contrast to the results in Staiger et al. (2010), means that firm-specific labor supply is quite elastic. One potential explanation for this discrepancy is that employers can choose to increase either their wage or their recruitment intensity in order to attract more workers (Manning, 2006).16 Under this set of assumptions, mandated changes to wages or employment might not allow researchers to identify the elasticity of labor supply to the firm (Manning, 2011).
Another set of studies returns to the older question in the literature on the effect of employer consolidation in the health care labor market. Specifically, this set of papers examines how employer consolidation through mergers influences outcomes for both hospitals and their workers. Dranove and Lindrooth (2003) focus on the effect of mergers on costs and estimate mixed effects on wages following consolidation into health systems, with different effects being driven by the extent to which the merging entities also integrated their operational practices. Currie et al. (2005), meanwhile, study hospital consolidation in California during the 1990s with a focus on the wages and employment levels of nurses. They find no effect on wages but an increase in nurse effort (as captured by patient-nurse staffing ratios), which is consistent with a negative effect on quality-adjusted wages. They argue that influencing nurse effort may be an important non-wage mechanism possessed by firms in a model of monopsony that directly accounts for such a channel. Finally, DePasquale (2018) finds no effects on wages but negative effects on employment following some types of hospital mergers.
While these studies all focus on the specific parties to mergers in the health care industry, Prager and Schmitt (2021) use employer consolidation as a source of variation in employer concentration for the entire labor market. Their study can therefore be viewed as an industry-specific study comparable to Benmelech et al. (2020) and Arnold (2021). Prager and Schmitt (2021) find narrow evidence consistent with concentration as a source of labor market power. Specifically, they compare wage growth among health care workers in local labor markets (defined as commuting zones) that experience a merger which increases concentration with wage growth among similar workers in local labor markets without mergers. The authors separately report estimates by worker skill group and the magnitude of the change in concentration following a merger. They find no effect on wages among workers with relatively fewer skills in non-health care specific occupations (such as cafeteria workers). This null effect for these workers is present after mergers that increase employer concentration the most and is consistent with models of monopsony in which employers derive market power either through their size or search frictions. Intuitively, hospital mergers do not represent meaningful changes in employment opportunities for these workers because their skills and experience are easily transferable to other industries. For workers with relatively more skills, mergers in the top quartile of concentration changes caused wages to be 4.0% lower for those in non-health care occupations (such as human resources personnel) and 6.8% lower for nurses and pharmacy workers. These point estimates correspond to reductions in wage growth of approximately 25% from baseline.
While these wage effects are consistent with narrow but relatively substantial employer power in the labor market, the authors also perform other analyses which further make the case. First, they test for wage effects following mergers that involve hospitals in non-overlapping labor markets (where market power should therefore not be relevant) and find no effects for workers of any skill level or industry applicability and no effects in markets with different amounts of concentration before the merger. This finding convincingly shows that the wage effects following mergers between hospitals within the same labor market are not, for example, the result of changes in managerial practices. Second, the authors find that both higher levels of unionization and the absence of so-called right-to-work laws mitigate the negative wage effects of mergers.
Finally, Prager and Schmitt (2021) also provide some suggestive evidence for how this employer power arises in the first place. They differentiate between size-based power in which employers restrict employment below the competitive equilibrium level, and power derived from search frictions and bargaining. Their test involves estimating their same difference-in-difference models with employment levels as the outcome variable, and they find no evidence of changes to employment. The authors interpret this result to mean that search frictions and bargaining play at least some role in the employer power they have found.17
Labor market concentration is one potential source of employer power in the labor market. It is also an appealing way to characterize the degree of this power because consolidation that reduces the number of competitors in the market has straightforward implications for workers, it is easier to measure concentration than the standard indicator for monopsony power (the elasticity of labor supply to the firm), and it is directly connected to policy intervention through antitrust enforcement. These advantages of concentration, however, come with substantial challenges that researchers must overcome before making claims about how increases in concentration affect competition among employers and wages for workers.
In particular, researchers must be careful to describe the relationship between concentration and wages as correlational rather than causal. The need for such care is due to the fact that both concentration and wages are the result of market forces. This joint determination between concentration and wages has led researchers to use a variety of instrumental variables for local concentration. However, most of the existing instruments lack a theoretical justification for why a given change in concentration would affect wages because of an increase in employer market power and not because of other factors, such as changes in productivity or costs. The use of mergers and acquisitions can help solve some of these challenges, but, as discussed above, these events account for only a small fraction of all changes in concentration (Arnold, 2021).
The most compelling research designs discussed above also perform additional tests for whether a given change in concentration affects wages because of changes in employer bargaining power. For example, both Benmelech et al. (2020) and Prager and Schmitt (2021) find that a larger union presence in local labor markets dampens the negative effects of mergers, which supports the hypothesis that these consolidations are at least partially impacting labor market power. Focusing more specifically on the health care industry, Prager and Schmitt (2021) nicely lay out theoretical justifications for why certain types of workers would or would not be affected by employer consolidation if the hospital mergers they study were to increase monopsony power in local labor markets. The authors then show results consistent with these predictions, further strengthening their argument that hospital mergers very likely increase employer power over certain types of workers.
The lessons from the recent literature for researchers interested in using local concentration to study monopsony are numerous and potentially not fully satisfactory. Essentially all existing research designs are unable to make causal claims about the relationship between concentration and wages, necessitating additional tests to support ones claims and refute alternative explanations. While all of these studies use instruments for concentration in an attempt to overcome problems with the inter-relatedness of concentration and wages, these instruments cannot eliminate all of these issues. Studies of a single industry, such as health care, have real benefits over those concerning multiple industries because it is easier for researchers to argue that their findings are not driven by non-labor market mechanisms. However, single industry studies are inherently limited in their ability to speak to other sectors let alone the economy as a whole. Local concentration, therefore, can be used effectively in the study of monopsony provided that researchers are careful to avoid common challenges and build their arguments around a variety of supportive evidence.
Arnold, David (2021), “Mergers and acquisitions, local labor market concentration, and worker outcomes.” Working Paper.
Azar, José, Emiliano Huet-Vaughn, Ioana Marinescu, Bledi Taska, and Till von Wachter (2019a), “Minimum wage employment effects and labor market concentration.” Working Paper.
Azar, José, Ioana Marinescu, and Marshall Steinbaum (2019b), “Measuring labor market power two ways.” AEA Papers and Proceedings, 109: 317-321.
Azar, José, Ioana Marinescu, Marshall Steinbaum, and Bledi Taska (2020a), “Concentration in U.S. labor markets: Evidence from online vacancy data.” Labour Economics, 66, 101886.
Azar, José, Ioana Marinescu, and Marshall I. Steinbaum (2020b), “Labor market concentration.” Journal of Human Resources, Forthcoming.
Bassier, Ihsaan, Arindrajit Dube, and Suresh Naidu (2021), “Monopsony in movers: The elasticity of labor supply to firm wage policies.” Journal of Human Resources, Forthcoming.
Benmelech, Efraim, Nittai K. Bergman, and Hyunseob Kim (2020), “Strong employers and weak employees: How does employer concentration affect wages?” Journal of Human Resources, Forthcoming.
Berger, David W, Kyle F Herkenhoff, and Simon Mongey (2021), “Labor market power.” American Economic Review, Forthcoming.
Boal, William M. and Michael R Ransom (1997), “Monopsony in the labor market.” Journal of Economic Literature, 35: 86-112.
Bresnahan, Timothy (1989), “Chapter 17: Empirical Studies of Industries with Market Power.” Handbook of Industrial Organization, Vol 2 (Richard Schmalensee and Robert Willig, eds.), North Holland, pp. 1011-1057.
Bronfenbrenner, Martin (1956), “Potential monopsony in labor markets.” ILR Review, 9: 577-588.
Burdett, Kenneth and Dale T. Mortensen (1998), “Wage differentials, employer size, and unemployment.” International Economic Review, 39: 257-273.
Currie, Janet, Mehdi Farsi, and W. Bentley Macleod (2005), “Cut to the bone? Hospital takeovers and nurse employment contracts.” ILR Review, 58: 471-493.
DePasquale, Christina (2018), “Heterogeneity in hospital consolidation.” Working Paper.
Dodini, Samuel, Michael F. Lovenheim, Kjell G. Salvanes, and Alexander Willén (2020), “Monopsony, skills, and labor market concentration.” Working Paper.
Dranove, David and Richard Lindrooth (2003), “Hospital consolidation and costs: another look at the evidence.” Journal of Health Economics, 22: 983-997.
Falch, Torberg (2010), “The elasticity of labor supply at the establishment level.” Journal of Labor Economics, 28: 237-266.
Felix, Mayara (2021), “Trade, Labor Market Concentration, and Wages.” Working Paper.
Hershbein, Brad, Claudia Macaluso, and Chen Yeh (2020), “Monopsony in the U.S. labor market.” Working Paper.
Jarosch, Gregor, Jan Sebastian Nimczik, and Isaac Sorkin (2019), “Granular search, market structure, and wages.” Working Paper 26239, National Bureau of Economic Research.
Lamadon, Thibaut, Magne Mogstad, and Bradley Setzler (2021), “Imperfect competition, compensating differentials and rent sharing in the U.S. labor market.” Working Paper.
Lipsius, Ben (2018), “Labor market concentration does not explain the falling labor share.” Working Paper.
Manning, Alan (2003), Monopsony in Motion: Imperfect Competition in Labor Markets. Princeton University Press, Princeton, New Jersey.
Manning, Alan (2006), “A generalised model of monopsony.” The Economic Journal, 116: 84-100.
Manning, Alan (2011), “Imperfect competition in the labor market.” Handbook of Labor Economics, 4: 973-1041.
Manning, Alan (2021), “Monopsony in labor markets: A review.” ILR Review, 74: 3-26.
Marinescu, Ioana, Ivan Ouss, and Louis-Daniel Pape (2021), “Wages, hires, and labor market concentration.” Journal of Economic Behavior & Organization, 184: 506-605.
Matsudaira, Jordan D. (2014a), “The elasticity of labor supply at the establishment level.” Review of Economics and Statistics, 96: 92-102.
Matsudaira, Jordan D. (2014b), “Monopsony in health labor markets.” In Encyclopedia of Health Economics (Anthony J. Culyer, ed.), 325-333, Elsevier, San Diego.
Miller, Nathan, Steven Berry, Fiona Scott Morton, Jonathan Baker, Timothy Bresnahan, Martin Gaynor, Richard Gilbert, George Hay, Ginger Jin, Bruce Kobayashi, Francine Lafontaine, James Levinsohn, Leslie Marx, John Mayo, Aviv Nevo, Ariel Pakes, Nancy Rose, Daniel Rubinfeld, Steven Salop, Marius Schwartz, Katja Seim, Carl Shapiro, Howard Shelanski, David Sibley, and Andrew Sweeting (2021), “On The Misuse of Regressions of Price on the HHI in Merger Review.” Working Paper.
Nimczik, Jan Sebastian (2020), “Job mobility networks and data-driven labor markets.” Working Paper.
Prager, Elena and Matt Schmitt (2021), “Employer consolidation and wages: Evidence from hospitals.” American Economic Review, 111: 397-427.
Qiu, Yue and Aaron J. Sojourner (2019), “Labor-market concentration and labor compensation.” IZA Discussion Papers 12089, Institute of Labor Economics.
Rinz, Kevin (2020), “Labor market concentration, earnings, and inequality.” Journal of Human Resources. Forthcoming
Schubert, Gregor, Anna Stansbury, and Bledi Taska (2021), “Employer concentration and outside options.” Working Paper.
Sokolova, Anna and Todd Sorensen (2021), “Monopsony in labor markets: A meta-analysis.” ILR Review, 74: 27-55.
Staiger, Douglas O., Joanne Spetz, and Ciaran S. Phibbs (2010), “Is there monopsony in the labor market? evidence from a natural experiment.” Journal of Labor Economics, 28: 211-236.
Syverson, Chad (2019), “Macroeconomics and market power: Facts, potential explanations, and open questions.” Journal of Economic Perspectives, 33: 23-43.
U.S. Department of Justice (2018), “Herfindahl-Hirschman Index.” https://www.justice.gov/atr/herfindahl-hirschman-index, accessed September 14, 2021.
Wiltshire, Justin C. (2021), “Walmart Supercenters and Monopsony Power: How a Large, Low-Wage Employer Impacts Local Labor Markets.” Working Paper.